Minimalism Pre-Prints 3: Structure, Repetition, and Reception in Einstein on the Beach (2)

Note

Please see the Preface to this Series to understand the goals of putting up this unpublished work and the general apologies for not citing a more up-to-date bibliography.

This paper is a (mostly unedited) seminar paper presented to Reinhold Brinkmann's seminar on twentieth-century opera (Fall 1999). Thus no bibliography or citations post 1999 are included.  It was also written at a time when many musicologists could have not known the basics of Einstein; now this view seems a little obsolete. The only changes (beyond fixing of typos) in this version are the YouTube clips that have been added where easily found.

It Could Be Very Fresh: 

Structure, Repetition, and Reception in Einstein on the Beach (1999; part 2)

Glass's Analysis

Glass has chosen to base much of his analysis of the work on the harmonic features of the music.  The introduction of harmonic shifts within sections, begun with Music in Twelve Parts (1971-4) and continued in Another Look at Harmony (1975) which Einstein grew out of was for Glass a significant change in his musical style in the years preceding the opera.  It is understandable that since most common tools for analyzing Western music rely on harmonic structure he would employ these methods in looking at his own now harmonically shifting works.¹³  However, a look at Glass’s harmonic analysis of a single motive, five, reveals how little roman numeral analysis of his motivic idea tells us about the work.

¹³ Other conventional analytical tools would present other problems; Schenkerian and other voice-leading analysis techniques, even if they were available to a composer who received his musical training in the 1950s, can readily be seen to hold little promise for understanding this work.

If as Glass has said “process here is the subject rather than the source of the music” and “the noticing of process itself becomes exhilarating,”¹⁴ then an analysis which focuses on one iteration of a process is missing some of the most salient features of the piece.  Glass has pointed out that the motive, f-minor, D-major, A-major, B-dominant⁷, E-major can be heard as i-VI-IV♭ in f with IV♭ being heard as a pivot to IV-V-I in E.  He has further stated that since the motive ends a half-step below where it began it “provides the leading tone for the original i (f).  As it is a formula which invites repetition, it is particularly suited to my kind of musical thinking.”¹⁵

¹⁴ Robert Wilson and Philip Glass, Einstein on the Beach, edited by Vicky Alliata, (New York : EOS Enterprises, 1976(?)), [n.p., center of book]. The quotations sound more like Reich than what we are used to hearing from Glass in their emphasis on the perception of process.

¹⁵ Philip Glass, “Einstein on the Beach,” essay printed in liner notes to recordings of Einstein on the Beach and in Music by Philip Glass. Part 2, paragraph 6.

While he is correct in stating the five chords can be heard as a modulation from f minor to E major, it is certainly questionable whether any listener will hear it as such, or especially whether the twentieth repetition of the cell will produce such an effect on the listener.¹⁶  The ability to hear this passage tonally is particularly hampered by the voice-leading from the fifth chord to the first chord of the repetition.  While the other four transitions between chords followed traditional four-part voice-leading rules,¹⁷ the motion from E major to f minor contains three major “errors”: There are parallel octaves between the “alto” and “bass” voices, parallel fifths between the “tenor” and “bass”, and a doubled leading tone.  After hearing this non-common practice transition, it is unlikely that the listener will perceive further repetitions tonally; the use of IV♭ as a pivot chord was already a stretch to hear the first time.

¹⁶ The sections of five in “Train 1” have 39 repetitions each. “Knee 2” has 44 repetitions of five (22 + 22). The 158 repetitions in “Spaceship” dwarf any other section of five in the opera. I will be using the term “cell” to refer to a specific instance of a motive in which the motive may be rhythmically or melodically altered.

¹⁷ This statement notes but takes exception to the doubling of the bass a fifth higher which, everywhere except in the score, is heard as an acoustical effect of the electric organs and not an independent voice.

If we do not hear this progression as a tonal modulation (at least after the first presentation) it makes sense to ask whether Glass’s choice of chords has any bearing on our perception of the music.  I will argue that does using two alternative versions as counter-examples:

Purely tonal variation

Non-tonal variation

The version above is a strictly tonal version of five, grounded in E major.  The lower version is an atonal rendition of the theme, not cadencing in any key.  Both versions preserve the general bass contour of five, use triadic harmony, and retain three of the chords of five.¹⁸  Yet neither alternative is satisfying under repetition the way five can be heard to be.  In the tonal version the listener becomes frustrated because there is a strong unfulfilled expectation that the music will “go somewhere” harmonically yet there is a feeling of sameness because the music does not—it is simply E major followed by E major.  The atonal version distances the listener for the opposite reasons.  Without any cadential formula there is no harmonic expectation created and little (harmonic) reason to continue concentrating on the music.  It is the version in Einstein which balances these listening concerns.  The final three chords (IV-V⁷-I) form the most efficient establishment of tonal center possible while the augmented triad formed by the first three is an effective way of eliminating a possible key—the only triad not able to be constructed from diatonic scales.¹⁹  The listener tries to make tonal sense of the progression only to realize in the next repetition that this is futile.  Later, the strength of the IV-V⁷-I cadence invites him or her to try again, repeating the process many times throughout the piece.

¹⁸ With the hindsight of knowing his future output, one might wonder if the atonal version is actually a plausible alternative Glass could have written. It should be remembered, however, that in 1976 the last major work by Glass was Music in Twelve Parts which ended with a complete twelve-tone row in the bass.

¹⁹ Another piece from the 1970s which achieves its harmonic interest through a contrast between two contrasting harmonic areas within a repetition is Reich’s Four Organs (1970). An example of a piece which uses harmonic material related to the “atonal” theme is Louis Andriessen’s Hoketus (1977), sections A-D. As in the alternative Einstein version, the two and later four non-tonally directional chords of Hoketus cause the listener not to derive interest from the pitches played within a section. In Andriessen’s work this is intentional and a way of directing the listener toward the rhythmic and antiphonal features of the piece.

These harmonic aspects of the motive, while containing some interest in themselves, are subservient to the process of development the cell undertakes over time.  When presented as part of the train “still-lives” (Train 1, Night Train, the coda of Building, and Spaceship), each of the five chords has a different meter which changes throughout the section.²⁰  This is the process of primary musical interest:

²⁰ In the knee plays, five maintains a constant meter within a repetition but changes meter between repetitions. This process as carried out in “Knee 4” is examined below.

The numbers in the table represent the number of eighth notes in each cell.  A few characteristics of the rhythmic process are immediately apparent.  From section B to K, with the exception of the fourth chord of F all rhythmic processes are strictly prolonging.  Each repetition chord is as long or longer than the previous repetition of it.  Another property of the process is that each chord is held for either 3♪, 4♪, (3+3)♪, or (4+3)♪ . ; that is to say, the chords with 6 or 7♪ introduce no new figurations not heard in the 3 or 4♪ sections.²¹

²¹ Later presentations of five will be have lengths of 5♪ and 8♪ (Knee 3) and will have 6♪ figures which are not literal repetitions of 3♪ (see "Knee 4," second cell, below).

The lengthening of chords (and thus cells) follows two distinct processes and thus divide the section.  The first cell, A (repeated three times) acts as an introduction and a presentation of what becomes the standard form of the motive—when five is heard at the end of “Building,” A is the only form presented.  The next five cells, B-F, present the process of lengthening the motive from 3♪ to 4♪ beginning with the fifth chord and progressing toward the first.  Cell F alters the process slightly by reducing the fourth chord to 3♪ while augmenting the first to 4♪.  Avoidance of the projection of regular meter within a cell seems to be the overriding reason for this decision.

The next five cells, G-K, present a similar process, lengthening from 4 (or 3) eighth notes (via 6♪ ) to 7♪ beginning with the first chord and moving roughly from front to back: 1, 2, 4, 3, 5.  The cell which at B lasted 16♪ is expanded by K to 33♪.  The shift back to the quick transitions between chords of L feels like a tightly stretched rubber band being suddenly released.  Without a change of tempo, the speed of the cell has been dramatically increased and, with the return of the rhythmic profile of the introduction, the process feels complete.  By repeating L six times rather than three Glass makes the coda more satisfying to the listener: while each chord is much faster (3 or 4♪ rather than 6 or 7♪), by the fourth repeat (which does not exist in any other cell) we are able to hear the cell not as a five-chord motive but as two five-chord motives, a total of 36♪.  Thus rather than lessening the tension of increased cell length (B-K), L acts as a culmination of this process.  By focusing our aural “gaze” on two different levels of activity, the pattern can be heard as both accelerating and broadening simultaneously and without contradiction.

(The analysis of Einstein will continue in the next blog post)

Minimalism Pre-Prints 2: Structure, Repetition, and Reception in Einstein on the Beach (1)

Note

Please see the Preface to this Series to understand the goals of putting up this unpublished work and the general apologies for not citing a more up-to-date bibliography.

This paper is a (mostly unedited) seminar paper presented to Reinhold Brinkmann's seminar on twentieth-century opera (Fall 1999). Thus no bibliography or citations post 1999 are included.  It was also written at a time when many musicologists could have not known the basics of Einstein; now this view seems a little obsolete. The only changes (beyond fixing of typos) in this version are the YouTube clips that have been added where easily found.

It Could Be Very Fresh: 

Structure, Repetition, and Reception in Einstein on the Beach (1999; part 1)

December 1976 witnessed the dropping of a new work, startlingly unusual in many ways, on a mostly unsuspecting Metropolitan Opera public.  Einstein on the Beach, a collaborative opera by artist/director Robert Wilson and composer Philip Glass brought the worlds of extreme avant-garde theater and repetitive minimalist music to the conservative opera hall for the first time.  Five hours without intermissions, omitting identifiable characters or narrative structures, and based on a tiny melodic and harmonic vocabulary, Einstein’s fundamental elements had all been developed in experimental theatre and music during the previous decade, but their union in Glass and Wilson’s opera resulted in a work whose impact has changed new music and especially new opera for the last quarter-century.

This paper asks what this impact has been and why this work has come to have such an influence.  It is an attempt to explain some of how Einstein works and how the piece came to exist at this point in Glass and Wilson’s creative output.  To present this study, some new and slightly unusual analytical tools are employed which rest on my ideas about how we listen to and perceive minimalist music.  While there is certainly not space to even attempt at a complete analysis of the work, it is my goal to use examination of a few representative sections to get at some of the underlying structures of Einstein, an opera I see as, if not flawless or totally without precedent, nonetheless remarkable and original in its musical and theatrical conception.

Structure of the Opera

Any analysis of the musical structure of Einstein must begin with Glass’s own comments on the subject given in the essay “Einstein on the Beach”, included in both recordings of the work.  In his essay, Glass describes the opera as being divided into sections defined by the number of distinct chords in them.  The opening “Knee 1” is obviously a three-chord section, A minor, G major,¹ C major.  Glass asserts that sections from one chord (Trial 1) to five chords (Spaceship and similar sections) are present in the opera.²  While an examination of the score according to tonal conceptions supports his arguments, whether the listener actually perceives changes in the pitch content of chords as the primary organizing feature of the music will be examined and challenged below.

¹ We do not know for certain that this chord is major until it appears in altered form in Knee 3 and 4 and in the recap in Knee 5. The dominant-tonic motion suggested by G-C allows us to hear G-major in the absence of evidence to the contrary.


² Throughout this paper, small caps will be used to denote motives in the opera. These motives can be found in charts in the appendix.

Addition of Wilson's Comment

Wilson has stated that his musical theater has its roots in the visual arts—especially painting and drawing.  As such, he has organized his use of theatrical space according to the way space is used in three different styles of painting: portrait, still-life, and landscape.  In a portrait, the focus of the observer is nearly completely taken in by the subject.  A still-life, while still having a main subject, derives much of its visual force through the relationship between that subject and the sounding context.  A landscape takes this sounding region and makes it the subject; while there may be different levels of foreground and background within a landscape, there is not a sharp distinction between subject and context as there is in the other two forms.

Wilson applied these concepts to Einstein by distinguishing three different uses of the stage.  He treated the knee plays as portraits: the action is limited to a small part of the stage, the actors are the focus of the scene, and what little “scenery” there is consists of chairs, slabs of glass, etc. at the same spatial distance as the actors.  The train and trial scenes (including “Building” and “Spaceship”) form the second of Wilson’s three divisions of theatrical space.  Actors are seen in relation to larger backdrops at the back of the stage and smaller props are placed throughout the stage.  The longer title of the two dance scenes, “field with spaceship” confirms their place as the two landscape sections of the opera.³  The entire field of the stage is used as the dancers move about causing the viewer’s eyes to continually shift from one actor to another.

³ There would be some question whether the spaceship scene in Act IV is also a landscape had Wilson not stated (in Einstein on the Beach, the Changing Image of Opera, 1986) that there were only two landscape scenes in the opera. Although the entire stage is used in “Spaceship” and the back of the stage, rather than being a backdrop, forms an integral part of the action (the musicians are placed there), the isolation of action in only a few places on stage at any particular moment distinguishes it from the other dance works.

Wilson’s portraits, still-lives, and landscapes are distributed symmetrically throughout the opera:

The opera can be symmetrically divided in several ways.  First, the knee plays divide the opera into four parts—the four acts—each of which contains two or three still-lives or landscapes.⁴  The landscapes divide the opera again into three sections as bracketed in the figure above.  The titles in italics are grouped together by their similarity in style: texts based on counted quarter notes.  These sections further divide the opera into two sections.

³ The musical material in “Building” and “Spaceship,” being derived from “Train 1” allows us to consider them as a unified section interrupted by “Bed.” With this conception, the symmetry is preserved to an ever greater degree.

The division of the opera into five knee plays,⁵ four acts, three sections articulated by Wilson’s “landscapes,” two sections divided by the recurrence of the counted quarter notes in “Prison,” and one unity parallels Glass’s contention that the musical material is made up of sections consisting of five, four, three, two, and one chord.  The symmetric divisions of the opera stand in contrast to the asymmetric rhythms and phrases of much of the work, reversing the standard of Western classical music.

⁵ Glass has stated that the most important musical material is introduced in the knee plays and has asserted that their structure structures the opera. Although I do not agree entirely with this statement, it is supported by the parallelism indicated above.

Visual and Non-musical Structures

Wilson and Glass have emphasized that they conceived of Einstein on the Beach as a “portrait” opera, where the scenes and staging would be composed of elements which related to the subject, Albert Einstein.  By choosing one of the most well-known and important figures of the twentieth century—the figure of the century according to Time magazine—the two creators did not need to present the story of a person’s life, but instead to present images on the stage and allow the audience to relate these images to the knowledge of the subject that they brought with them to the piece.  Musically, this took the form of a solo violin in the orchestra, since Einstein was a violinist, and possibly the prominent use of numbers as a foundation for the sung text.⁶  The visual references to Einstein are both more numerous and more difficult to connect to the subject.⁷  While other commentators have identified many of the references to his biography, references to his work in physics have been much more elusive for writers.  K. Robert Schwarz, for example, identified the train, one of the most important symbols in Einstein as simply a vague reference “back to a pre-atomic era.”⁸ 

⁶ The numbers were not originally planned to be part of the sung text and were inserted for aid in memorization of rhythms. However, that they remained in the opera in the end and only in certain places argues for a connection between their presence and the subject of the work.

⁷ In many ways, they were also the most important for the first viewers of the opera, who came mostly to see a Wilson production and probably did not know SoHo’s Philip Glass. As John Rockwell wrote in 1978:

To be fair, ‘Einstein’ was a co-creation of Mr. Wilson and Philip Glass, the composer. But most people not only saw it as basically Mr. Wilson’s work—so much so that Mr. Glass was openly aggrieved, and has declined further collaboration with Mr. Wilson—but as the capstone to a series of remarkable large-scale Wilson theatrical creations that dated back to the 1960s. (New York Times, 26 November 1978, p. 5)

There is a certain irony that in America today the work is mostly viewed as not the capstone of Wilson’s creations but the starting block for Glass’s first operatic trilogy.

⁸ K. Robert Schwartz, Minimalists (London: Phaidon Press Ltd. 1996), p. 131.

The train meant far more than this for Einstein’s work in physics.  The train was a recurring subject in his explanations of special relativity, almost a leitmotiv for showing that the concept of simultaneity is not universal but particular to every observer.  The image Einstein evoked, which recurs in practically every physics textbook today, was that of a train car being struck by lightning at least twice:⁹

⁹ Examples from physics books are reproduced from Douglas C. Giancoli, Physics: Principles with Applications (Upper Saddle River, N.J.: Prentice Hall, 1997), however they could have been taken from any number of physics texts.

“Train 1,” a bar of light cuts through the train backdrop twice, in the sections where the process of cyclical motives of different lengths (cyc) gives way to music in E♭ based on additive processes (add).¹⁰  It certainly could not have escaped the notice of Glass that his musical stretching and contracting of our perception of time, through repetition and additive structures, was carried on against the backdrop of a proof that time has no absolute reference point.

(2015: Video clip showing the striking of lightening on a train)

¹⁰ David Cunningham, “Einstein on the Beach,” Musics 12 (May 1977), reprinted in Writings on Glass (q.v.), pp. 155-156. Cunningham is one of the few writers to note the train’s importance in relativity demonstrations. He also recognized the allusion to Einstein’s question about riding on a beam of light in “Spaceship”.

The transformations of the train into building and spaceship in Act 4 also have their roots in relativity thought experiments.  The building, seen from both the front and side simultaneously, is a demonstration of how observers at rest see light reflected off objects moving at high speeds.¹¹

¹¹ I have photo-reversed the image of the building from the opera to make the similarity to the physics text’s diagram. Note that the front of the building is not rotated in either image, the important distinction between a relativity demonstration and a standard perspective drawing.

The spaceship image, in addition to being a standard demonstration of relativistic length contraction (along with a rotating ruler or stick or an oblong clock which are also seen in the opera) hints at the prospects for future nuclear apocalypse which Einstein’s work on nuclear physics made a frightening possibility.¹²

¹² Glass, in Music by Philip Glass, has denied that Nevil Shute’s 1957 post-apocalyptic novel On the Beach was a conscious influence on Glass or Wilson. There are several other music compositions having “on the beach” in their titles which could have influenced Glass (and possibly even Wilson’s) choice of titles. The second movement of Ralph Vaughn William’s Sea Symphony (c. 1909) is titled “On the Beach at Night Alone.” The similarly titled “On the Beach at Night” by Andrew Imbrie (1961) is scored for vocal ensemble with string orchestra. Roger Session’s song “On the Beach at Fontana,” (1967) taking its words from James Joyce, is another possible influence. All three of these works begin “on the beach at” somewhere, which is a closer parallel to the opera’s original title, “Einstein on the Beach at Wall Street” than is the Shute novel. The connections are unlikely, but Glass and Wilson would be the last to deny that meaning in the opera could be constructed for a listener via past experience with the novel.

The length contraction demonstrated by the spaceship manifests itself in several other ways in the opera.  The tall, narrow chairs used throughout the opera are examples of this physical phenomenon on stage.  Further analysis of how the staging parallels the teachings and life of Einstein will have to await a video viewing of the opera.

(The paper will continue in a coming blog post with musical analysis of the opera. The "further analysis," even several live and video viewings later will still need to wait.)

Minimalism Pre-Prints 1: Ambiguity and Certainty in Minimalist Processes

Preface

From 1998 to 2006, I worked extensively on Minimalist music as a secondary field to my main research on fourteenth-century music. Under the caring guidance of Reinhold Brinkmann, I gave several papers on the topic, considering a dissertation on Glass's Einstein on the Beach and the analysis of minimalist music. 

By the end of my Ph.D., I had three mostly written articles which needed the sort of fleshing out to turn conference paper into publication. Good events, such as having many obligations at MIT, discovering computational musicology/music21, and having more to say on medieval music, conspired to make it so these articles never got polished nor made it into print in any way beyond the few people who still had handouts from random conferences where I presented the work.

It is nearly 2016 and I have not worked in minimalist circles for almost ten years now. During this time, minimalist studies have exploded: the Society for Minimalist Music has been founded, numerous conferences have taken place, and whole monographs on significant works such as Nixon in China, De Staat, and so on have been published. Minimalism has gone from being a research area to sneer at to one of the foundational parts of modern music studies. Thus, my work was becoming more and more dated with each year that I did not keep up with new bibliography, new terminology, and new discoveries.

It has become time to admit that it's extremely unlikely that I will ever work up these thoughts into a format that could be published in a significant journal. I can already imagine the "revise and resubmit" requests to cite so many people whose work is relevant to my own, but which I don't know now and was not written when I wrote the words below. I have tenure now, so formal publication is less important to my career than it was a couple of years ago. Yet I do think that there are probably some tidbits of theories here that might still be useful to someone. What I present below are unrevised (except in the case of typos or sentences that trailed off or references to video clips etc.) versions of talks given between 1999 and 2005. I would welcome comments on places where I can add bibliography and cite others who published this work first  (which I will update with a note) and I apologize in advance for all the already published work that is not included. If there is interest (by a journal that does not mind that this has appeared on the web), I could revise later, but none of this information was doing anyone any good sitting on my hard drive, so might as well get it up where maybe it could help someone.

Given the best traditions of blogging, I will try to break these posts into approximately 1,000 word chunks. The label "minimalist publication project" will help find other contributions to this series as they are uploaded.

Ambiguity and Certainty in Minimalist Processes

Dublin Conference on Music Analysis, June 2005

A useful way of looking at repeated processes in minimalist music is to consider the amount of ambiguity or certainty they introduce.  This view moves beyond description of the mechanisms of processes (additive, divisive, cyclic) and focuses on their effects on the form of a work or a section of a work, and from there on the expectations of listeners.  I begin by discussing how some processes have the potential to create ambiguities in perception.  We will then observe the opposite case: pieces where we are able to perceive order in the midst of a highly complex or seemingly somewhat homogenous texture.

(2015): The paper began with several definitions of process in minimalism which were given in expanded form in other articles. They will be put in a separate post. It ended with discussions of process in Lucier and Beethoven, which will also be put in a separate post. What remains here are the elements of the paper that fit into the narrow niche of Ambiguity and Certainty.  For this reason, Figure numbers do not begin at 1.

I’m mostly going to confine myself to “top 40” minimalist pieces; the hits, in order to keep things in more familiar territory.  Let us consider a passage from Glass and Wilson’s Einstein on the Beach, given in a modified score as Figure 4.  The music is taken from the connecting passage between the first and second acts, Knee Play 2.

In this section, a series of additive and subtractive processes augment and diminish the lengths of the arpeggios. Let me focus on one place where I believe a clearly defined process can produce ambiguous results.

I believe no matter what, we have to hear the passage as a gradual change in tempo.  But we are given the opportunity to choose among two or more different tempo progressions.  In one of these ways of hearing, the beat of the passage is tied to the repetition of contour and its emphasis on the repeated bass note.  In this mode of listening, lines two and three have more but faster beats than the preceding lines.  This process is described by the line marked "contour" in Figure 5  What we hear is a subtractive process—a quickening of the tempo from six eighth notes per five beat section to four eighth notes per ten beat section.  The process continues now by removing a single eighth note and playing fifteen three-note beats per repetition.  Then one further eighth note is removed and we are left with two-note beats.⁴

⁴ After the two eighth-note contour, I have chosen six eighth notes to be the fundamental motivic beat for the final line of Figure 5's contour analysis rather than the one eighth-note beat. This choice was based on research that showed that tempos near to or father than 300 beats per minute are usually unable to be perceived as beats. See, for instance, Simon Dixon, "Automatic Extraction of Tempo and Beat from Expressive Performances," Journal of New Music Research 30 (2001).

Intriguingly, many listeners hear the passage in the opposite way, emphasizing the chord changes as primary over the repetition of contour. This hearing is given in the line marked "harmony" in Figure 5.  In this way of listening, the passage is primarily a large-scale ritardando except for the motion between passage 3 and passage 4 which is unambiguously an acceleration of beat no matter which mode of listening is chosen.^*

^* (2007/2015) In seven talks and classroom presentations I have conducted an experiment where I asked listeners to tap silently along with the changing beat of Knee 2 before giving this section of the paper. The results were always nearly evenly divided between those who chose the contour interpretation of the beat and those who chose the harmonic interpretation (a few listeners could not find a beat at all). In later talks I asked listeners to identify whether or not they had absolute pitch after conducting the experiment. The minority of listeners with absolute pitch always chose the harmonic interpretation over the contour interpretation, perhaps suggesting that the relationship between two motives with similar contours but different harmonies is much weaker for absolute pitch possessors than for the general population. I have been wanting to reproduce this experiment in a more formalized setting, but I admit now that this is not going to happen any time soon. In an April 13, 2005 interview with Philip Glass I conducted in Rome, I asked him about the changing beat and he said, "You mean where it goes 6, 4, 3, 2." I mentioned that some people hear it as slowing down because of the chords and he replied with some surprise, "Really?" but then returned to calmness saying that it was not too surprising because he tried to put ambiguous interpretation into his works and told the Beckett story with which this paper continues. I want to publicly thank Philip Glass for being so generous with his time and for JoAnne Akalaitis for facilitating the interview.

Ambiguity was a fundamental part of Glass’s musical philosophy in writing Einstein—he has frequently stated that he admired the quality of Beckett’s drama that each listener could experience the epiphany of the work in a different place; yet it is rare that a quality so fundamental and usually simple such as tempo can be experienced in opposing ways by different listeners.  The balance that allows ambiguous perception is also fragile.  The addition of a chorus sustaining the chords when the material returns in Knee 4, for instance, emphasizes the ritardando interpretation.

Stronger accidents at the beginning of each repetition of contour could have the opposite effect.  Once the ambiguity in the passage is noticed, there is also the possibility of consciously or unconsciously switching-gears at any moment from the contour to the harmonic interpretation or back to create other paths of acceleration and deceleration.

In Einstein, we have an ordered and predictable process which can create ambiguities in hearing a fundamental part of the music, the beat.  Conversely, some composers have paired minimalist processes which create surface disorder with compositional decisions which limit ambiguity.  Frederic Rzewski’s Les Moutons de Panurge is a piece for any number of players on any instruments consisting of a single melodic line.  First only one note of the line is played, then two, three, and so on until all sixty-five notes are played, after which notes are removed.  See the score and the realization of the opening in Figure 6.

As normally performed, due to rhythmic errors in playing, the musicians will make mistakes that cause them to temporarily be off from one other. Unlike standard performance situations, where the musicians would then get back in sync, the score tells the musicians to remain off from the others, eventually creating a jumble of different layers.

Although the work uses only two rhythmic values (quarter and eighth notes) and simple diatonic intervals favoring stepwise motion and motion by thirds--in a word, simple--the melodic line is constructed with practically no repetitions among various sections. The line has enough distinct material that even very short melodic sections played by any musician and which jump out of the texture give enough information to identify where each instrument is in the melody. Figure 7 gives a list of the places where hearing two or more notes is insufficient to precisely locate a player within the sixty-five-note score.

There are fifteen two-note segments which do not identify the player's location. These represent thirty-three of the sixty-four possible two-note starting places, or about half.  If three contiguous notes can be heard from a single instrument in the texture, then there are only five segments that do not identify the location of the player. In fifty-five of the sixty-three possible places, the musician's position in the score will be known to the listener. With four contiguous notes, there are only two places of ambiguity, and with five notes, the listener always can have complete certainty of a musician's location.

I am not saying that Rzewski has purposely arranged his material to create maximum distinctiveness—in fact, I had a computer program generate 1000 random melodies, sharing only Rzewski’s notes and rhythms and his predilection for stepwise and 3rd motion, and the results were similar.⁵  The distinctiveness of short motives is not a result of his ordering, but rather of his choice of melodic material (non-tonally oriented skips and no apparent reason behind the choice of longer notes) and the lack of any distinctive ordering.  We can contrast the 65 notes of Moutons with the first 65 notes of the clarinet entrance of Mozart’s concerto.  Hearing any isolated note in Mozart’s work will give you a better idea of your location in the work, but there are many more locations where hearing three, four, or even five or six notes will not pinpoint your location.  A movement from a Bach solo ’cello suite would almost certainly have a lower level of distinctiveness by this metric.

⁵ A random distribution of the notes used by Rzewski was shuffled in a way that favored motion by seconds and third by having a 50% chance of reshuffling the notes if motion larger than a third was created, and a 75% chance of reshuffling if it was larger than a fourth. On average, this process resulted in 14 two-note matches per piece, 1 or 2 three-note matches per piece, a four-note match every six pieces, and a five-note match every fifty pieces

A similar effect can be heard in Satie’s oft-cited “proto-minimalist” work, Vexations, whose bass line is given in Figure 8.

Here Satie has composed the line out of extremely distinctive intervals, approaching the construction of an all-interval set.  Any two consecutive pitches or intervals in the bass will uniquely identify where the performer is within the line.  The piece is thus constantly sending signals about where the performer is in within this short line.  The larger form of the piece is completely different, consisting of 360 repetitions of this bass line organized into 840 larger repetitions played over 12 to 24 hours. Maddeningly, these interval-based signals constantly give localized information about the position in the line but give absolutely no information about where we are in the overall form of the work.

Ambiguities of perception and certainty within chaotic or hard to perceive processes are essential but overlooked components of minimalist music. Considering them in the light of previous characterizations of minimalist processes can bring out the many complexities hidden within seemingly simple pieces.

Peer-Review and Publication of Unprintable Materials

The following was a panel presentation given at the American Musicological Society meeting in Louisville, November 2015, as part of the discussion "Beyond the Printed Page: Electronic Publishing and its Implications for Musicology," sponsored by the Committee on Career-Related Issues, the Committee on Technology, and the Committee on Publications, organized by James V. Maiello.

In thinking about the future, I find it’s always helpful to reconsider the past.  What were the roles of publishing in the age of print and print only? Why was it important to have ideas published? Only publishers could get an idea out to a large audience that would want to read it. Publishers had distribution networks that could take it from a single location (the city that we still cite in footnotes) and make it available throughout the world. The publishers took on financial risk in printing and distributing material: if they did not print ideas that were worth reading, scholars and librarians would stop subscribing to journals or purchasing books, leaving them unsold inventory in the present and less influence in the future. The publishers’ sense of the market would give an idea of how much interest there would be in the idea while peer review would ensure the quality of that idea. Initially, the reputation of a journal or publisher would determine how many people purchased and read it. Later, public review would help individuals and libraries decide which material to pick up after the initial sales.

While people sometimes speak of electronic publishing, particularly open access publishing, as changing everything, some of the prior paradigms remain and some disappear. Costs in production have certainly changed: The costs of an online publication (rights, editing, hosting) are basically the same whether its distributed to one reader or a million. Access, in the case of OA publishing, has absolutely changed. I doubt there is a single person on earth who has access to a print journal such as Acta musicologica who doesn’t also have access to the Internet.

What hasn’t changed at all though is the mark of quality and reputation that one journal or press has over another. Perceived differences in reputation or importance for online vs. paper has largely to do with the newness of most online journals. If the Journal of the American Musicological Society or Oxford University Press started publishing exclusively online, I doubt they’d take any hit to their reputation. It’s the name and the history that determines the importance of what is published, not the method of distribution. This authority—bound to decades of (mostly) good decisions about what to publish—is what is generally lost with electronic publishing.

If this hypothesis be true, then one need ask how can journals and publishers use their authority and reputation to advance scholarship better through digital publishing. I’d like to call on journals and the Society to be more open to peer-reviewing and “publishing” born digital materials, especially data collections, such as image archives, score collections, and spreadsheets that are of particular value to the scholarly community. Such publications used to be common in Anglo-American scholarship and particularly on the European continent. Here’s an example of what used to be published: An article by Gilbert Reaney in Musica Disciplina, where the text is largely introduction and connecting tissue around the main contribution of the article: pages and pages of charts describing the actual contents of some new finds. 

Or this contribution by Claude Palisca to JAMS in the 1950s, whose second part largely consists of organized musical examples of a surprising nature extracted from a large counterpoint treatise.  

Yes, both articles have text, but what mainly was peer-reviewed and published was data and a short justification for the significance of this data.

You won’t find many articles like these published today. In part there’s been a backlash against perceived empiricism without theoretical reflection, a new direction for scholarship, and so on, but this is not all of it. A larger reason is that our data has gotten too big to publish on paper, economically.  The best theoretically grounded article still would never appear in a major journal if it included a 300-page chart. Relatively forward-thinking journals have started to sometimes offer these tables, etc. as digital appendices. That may be fine for some people, but sometimes the table is not the appendix: it’s the article; if anything, it’s the introductory text that’s the appendix. The tables, hopefully in an original layout, sortable, filterable, and in original formats, can be the main text.

There are other important contributions to scholarship that are not included in peer-reviewed publication not because of their lengths but their formats: video, interactive explorations, computer software, or raw music notation files (such a curated collection of all the parallel perfect consonances in Bach chorales).

JAMS has begun to open one part of the publishing process to digital projects: the public peer review. The “digital and multimedia scholarship” section since 2014 has reviewed scholarly contributions that have already been released publicly on the internet or through other means.  It is a valuable part of e-publishing, validating, though after the fact, scholarship in non-traditional forms; Ian Quinn’s review of my music21 toolkit helped my tenure committee understand it as a book-equivalent project.(Dmitri Tymoczko's review in Music Theory Online had a similar impact for the theory world). But not all digital projects are book-length and thus subject to public review. And many projects would benefit from the process of peer-review earlier. It may seem odd at first to open an issue of JAMS and see nothing but a title, author, one or two page introduction and a web link to the materiel of the publication, but it is a necessary step towards using publication to even out the playing field between traditional and newer forms of scholarship.

Given the sponsor of the session, and the importance of teaching in our careers, I’d like to end with an appeal to pedagogy. We try to teach our students to distinguish between good information and less reputable. Articles appearing in JSTOR tend to be pretty good; random websites turning up from a google search are more problematic. Yet, if there are whole classes of scholarship: digital projects, data sets, videos, that cannot be recommended due to lack of peer review, lack of a press or journal name attached to them, we are shutting out our students to many of the top fruits of our scholarly labor. I hope we can change that.

Errata: 2015-11-20: The original version of this post mistakenly identified the third committee sponsoring the session. It is the Committee on Publications. It also referred to a slide of parallel perfect consonances in Bach chorales that was not included. The text has been adjusted.

Merge upstream into your fork in GitHub

[Update: 12 August 2015: it is now possible to do this much more easily in the Beta version of GitHub Desktop]

For years I’ve been trying to get student assistants to use GitHub more effectively to work on larger projects.  One of the main problems though has been that the process of using forks + pull requests to submit their code to the main project has always required going back to the terminal for one key step: pulling and merging others’ changes from the upstream branches.  Today even for many seasoned programmers, the terminal/command prompt is a bit of a mystery to students.  Thus it would be great if the GitHub graphical client made this simple or at least possible.

The most recent versions of the GitHub client (at least on Mac; untested on Windows; I’m on v. 208) don’t exactly make the process simple, but at least they make it possible.

Open the GitHub client and if you haven’t worked on the project in a while, hit Sync. You should see your own fork; I’ll assume that you are working on the “master” branch and want to merge changes from the upstream (main project) master branch into your own branch.

Your screen should look something like this.  (I’ll be demoing on the amazing Latin dictionary program “whitakers-words”[*] which I do not have commit access on, so it’s like what my contributors to my projects would see).  All I’ve done is created a little demo text file.

Next I’ll pull down the tab on “master” and switch to the main developer’s master, “mk270/master” (third from bottom).


Click “Sync” in the upper left hand corner to copy it down.  The sync button will turn into a progress bar:

This actually creates a temporary branch confusingly called mscuthbert/mk270/master (or YOURNAME/THEIRNAME/BRANCH) but will just be displayed as mk270/master on the GitHub client.  No matter.  Now click the button next to the progress bar to create a pull request.  You will want to pull from this branch to your master branch (the one marked default branch):


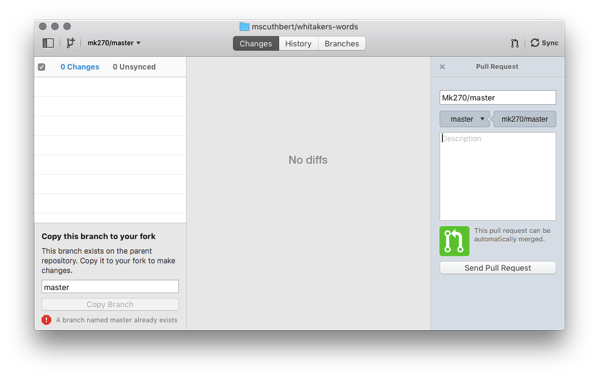
You can leave the description blank since you’re just making a pull request to yourself. Go ahead and click “Send Pull Request”.

Click the link below the “Good work!” button to open up GitHub in your browser.  You should see something like this:

Scroll down to the bottom and you’ll see this.  Go ahead and click “Merge pull request” then “Confirm merge”.


Now you’ll see the option to delete this branch.  Go ahead and do it.  You are actually deleting “mscuthbert/mk270/master” not “mk270/master” — I hope it won’t let you delete the upstream master!

After doing so you’ll see this confirmation.

Now return to the GitHub client and switch back to “master” if it hasn’t already put you back there.

Go ahead and click “Sync” again for good measure.  Then you can check your History and see that you have all the most recent upstream commits:

Ta-da! Well, assuming that there aren’t any conflicts or anything of that sort.  In a case like that you’ll probably still need to get out the ol’ command-line tools, so you will still need to be a bit familiar with them (or have a friend who can help you out). Hopefully the next version of GitHub for Mac/Windows will make this much easier. But for day-to-day work, it’s now possible to stay in sync with the main repository on a more regular basis for people who use the graphic interface tools almost exclusively.

[*] edit August 10: EEK! Autocorrect originally changed “Whitaker’s Words” to “Whiskers-Words” — Fixed!  That app only does Cat-latin (catin?): "maumo, maumare, maumavi, maumatus  V (1st)     1 1 [GXXEK]   — meow;” not what we want!

NL vs. AL leadoff hitters

 

Often while marveling at Ricky Henderson’s amazing stats, I wondered how much greater a leadoff hitter he would have been if he had spent his whole career in the National League.  He had 11,180 plate appearances in the AL but only 2,166 in the NL. In both leagues, the leadoff hitter leads off the first inning, but is not guaranteed to bat leadoff in any following inning. However, I figured that in the National League, batting after the pitcher, it’d be substantially more common that the person batting first in the order would get to lead off. The pitcher almost always makes an out, so I figured it’d be pretty common for him to make the third out (and because of situations where the eighth batter is walked to get to the pitcher, probably more common than one in three).  The eighth batter isn’t that strong in the AL, but a lot stronger than almost any NL pitcher.

I’ve been working off and on over the past two years (more off before getting tenure, more on after getting tenure) on an extremely flexible python toolkit for examining baseball games and it finally got to the state of development where I could test my findings.  I’m not ready to release the toolkit yet (it needs to be polished enough that I’m proud of it), but here’s the code I used to work:

  gc = games.GameCollection()

  gc.yearStart = 2000

  gc.yearEnd = 2014

  gc.usesDH = True

  allGames = gc.parse()

  totalPAs = 0

  totalLeadOffs = 0

  for g in allGames:

      for halfInning in g.halfInnings:

          for p in halfInning.plateAppearances:

              if p.battingOrder == 1:

                  totalPAs += 1

                  if p.plateAppearanceInInning == 1:

                      totalLeadOffs += 1

  print(totalPAs, totalLeadOffs, totalLeadOffs*100/totalPAs)

 

It gets a collection of games where the DH is used or not used, looks at each game, then at each half inning, then at each plate appearance. If the batter is #1, then it checks whether it’s the first appearance in the inning, then prints out the percentage of all batter #1 plate appearances which are leadoffs.  The results were surprising to me. 

	PAs	Leadoff	%
No DH	183,033	75,364	41.175
With DH	163,1781	63,451	38.885

The average difference in the percentage of leadoff plate appearances between the two leagues (accounting for interleague games) is only about 2.5%. This works out to about 15 PAs a year different for Ricky in his prime. So one hypothesis down, but many more to be investigated soon.

Don Giovanni Facebook Status Update