
31 December 2010
Changing Musical Time in the Renaissance and Today
The concepts of time, rhythm, and musical notation have changed dramatically from the Middle Ages to the Present. Music has slowed dramatically over the past millennium, and composers have repeatedly taken advantage of new resources. This pre-print of a short paper in honor of Joseph Connors documents this change and shows how it can affect how we think of nearly every piece written from 1100 to today. It concludes with an in-depth discussion of a piece from a particularly important moment in the history of notation, the lauda, O Regina from the manuscript Siena, Archivio di Stato, Fondo Vicariato di Gavorrano (1568-69), Ravi 3, giving the first transcription of this work with its unique notation. (.pdf 600k)


Labels:
medieval music,
musicology,
notation,
trecento
22 April 2010
Managing with no idea about random fluctuations
Ah, Jerry Manuel, "manager" of the Mets, is up to it again. Now he's suggesting that he will bench or move Jason Bay or David Wright for batting .241 and .240 after 54 and 50 at bats, respectively. Of course batting .240 after an amazingly huge sample size of 50 at bats definitely proves that you're doing terribly, right? I mean it's utterly inconceivable that a .280 or .300 batter would go through a 50 at-bat period where they batted that low.
Okay, enough sarcasm, let's run the statistics for Jason Bay. Here's a little program in python than can do it for us.
------
------
What do we learn? It turns out that if Jason Bay were a pure .300 hitter -- that is he had a 30% chance of getting a hit on every at bat, there's a 22% chance that he'd have an average as low as .241 after 54 at bats. If he were a decent .275 hitter, he'd have 35% chance of having an average that low.
The numbers are about the same (or even a bit more disappointing) for Wright, which surprised me. I would've thought 4 extra at bats would far more than cancel out one point of BA, but it doesn't because the last digit isn't significant yet! With 50 at bats, it's impossible for Wright to be slightly better than Bay by batting, say .242, because each hit still represents a BA difference of .020! If Wright had one more hit, he'd be batting a respectable .260. If one or two fewer, he'd be at .220 or .200 and probably already traded by the kinds of short-sighted people who get paid millions to run things that they don't understand. (see: Management, Mets [or most non-winning teams]).
The point isn't that Bay and Wright are great hitters going through bad times. They could have morphed into terrible terrible hitters who are lucky to even be batting the .240 that they have. The point is that we just don't know yet. And given the number of millions you're paying them based on prior performance, maybe, just maybe, it makes sense to let them play long enough so we can find out what's actually happening?
Addendum, 3 hours later: I originally decided to leave out a criticism of the utter stupidity of messing with an approach that is causing Wright to be leading the league in walks (with a .457 OBP), but nah, they deserve all the criticism they can get. So there you are.
Okay, enough sarcasm, let's run the statistics for Jason Bay. Here's a little program in python than can do it for us.
------
import random
l = 0
for k in range(1000):
i = 0.0
for j in range(54):
if random.random() < .300:
i += 1.0
if (i/54) < .241:
l += 1
print "%2.0f%%" % (l/10.0)
------
What do we learn? It turns out that if Jason Bay were a pure .300 hitter -- that is he had a 30% chance of getting a hit on every at bat, there's a 22% chance that he'd have an average as low as .241 after 54 at bats. If he were a decent .275 hitter, he'd have 35% chance of having an average that low.
The numbers are about the same (or even a bit more disappointing) for Wright, which surprised me. I would've thought 4 extra at bats would far more than cancel out one point of BA, but it doesn't because the last digit isn't significant yet! With 50 at bats, it's impossible for Wright to be slightly better than Bay by batting, say .242, because each hit still represents a BA difference of .020! If Wright had one more hit, he'd be batting a respectable .260. If one or two fewer, he'd be at .220 or .200 and probably already traded by the kinds of short-sighted people who get paid millions to run things that they don't understand. (see: Management, Mets [or most non-winning teams]).
The point isn't that Bay and Wright are great hitters going through bad times. They could have morphed into terrible terrible hitters who are lucky to even be batting the .240 that they have. The point is that we just don't know yet. And given the number of millions you're paying them based on prior performance, maybe, just maybe, it makes sense to let them play long enough so we can find out what's actually happening?
Addendum, 3 hours later: I originally decided to leave out a criticism of the utter stupidity of messing with an approach that is causing Wright to be leading the league in walks (with a .457 OBP), but nah, they deserve all the criticism they can get. So there you are.
Labels:
baseball,
python,
statistics
15 April 2010
Changing Musical Time Over the Past 1000 Years
One of the fundamental changes in the West’s conception of music over the previous millennium was the idea that music’s rhythm and meter could be precisely measured not in terms of seconds or minutes, nor in borrowed notions such as poetic feet, but in purely musical terminology like quarter notes or dotted eighth notes.[2] This new way of thinking is intimately connected to the rise of musical notation, and in particular, the use of notation to show relationships among two or more coordinated parts. Pitch needed its own vocabulary even in the era of unwritten music—-organs needed to be built; lyres tuned—-but the necessity of specific terminology for musical rhythm arose only when it was written down. And while the notation of pitch became largely standardized within the first few centuries of the last millennium to the point where undergraduate music students can (more or less) read pitch from thirteenth-century manuscripts, rhythmic notation remained unsettled much longer.
Seemingly from the first moment when music became measured (musica mensurata), it began to slow down. The earliest measured music, that of Leonin and Perotin, the twelfth and early-thirteenth century composers of Notre Dame, used the figure of the “long” as a basic value, to be paired up and combined into a maxima or duplex long, or to be divided into three breves. By the late thirteenth century, music had slowed to such an extent that the breve became the basic note value, and the semibreve, worth either one-half or one-third the value of the breve, sprang into use.[2] This word, semibreve, is still the most common name in the British world for the note that in the States is called the whole note. Because the process of slowing continued unabated, this note is now the longest value in frequent use. By the fourteenth century, the tempo of music had slowed sufficiently that a note even faster than the semibreve needed to be introduced. This note came to be called the minima or minim--still the British word for half note—-signifying that this was to be the minimum, that is, the final, indivisible smallest possible note. (The debates of the music theorists of the Trecento are echoed in the discussions of modern physics that postulate that time itself may move in discrete and indivisible minima, each lasting about 1/200,000,000,000,000,000,000,000,000,000,000,000,000,000,000th of a second.) But the force of the slowing trend could not be stopped: it was less than fifty years later that the first “semiminim” would appear. Its name embodies a contradiction, “half of the shortest possible note,” yet though it was an extremely fast note for its time, it eventually became our most basic beat, the quarter note.
The process of slowing itself slowed slightly during the fifteenth, sixteenth, and seventeenth centuries. Faster notes continued to be introduced, but the fundamental tempos of music changed little. There are exceptions, and in some of these cases the slowness of the fundamental beat and the speed of the shortest notes produced dramatic effects: tuplet 128th notes appear in Beethoven’s third piano concerto, 256th notes in a concerto by Vivaldi (F. IV. n. 5), and most exceptionally, 1024th notes (incorrectly notated as 2048th notes) in the little known “Toccata Grande Cromatica” from The Sylviad by Anthony Phillip Heinrich (ca. 1825), a piece that in its own continual slowing of the fundamental beat is a microcosm of all of the notated music history of the West.[3] (See Example 1).

Example 1: Anthony Phillip Heinrich, “Toccata Grande Cromatica,” excerpt, with 512th and 1024th notes (incorrectly notated as 1024th and 2048th notes) at the end of the example.
Between Perotin and Heinrich, there exists a range of time that is almost incomprehensible to our sense of how music unfolds. Within a single maxima, there are 1024 128th notes, and, as we have seen, even longer and shorter notes have occasionally been used. Example 2 shows (on a logarithmic scale) the amount of time various notes would take if they were all played at the same adagio tempo of one quarter note per second. Obviously it is absurd to use the entire range of note values in a single piece at a single tempo mark. In fact the pieces using the shortest notes tend to have the slowest tempos, and the contrary is true for pieces with the longest notes. But Figure 1 demonstrates the enormous pull towards expanding the range of rhythmic resources that composers have felt over the centuries.
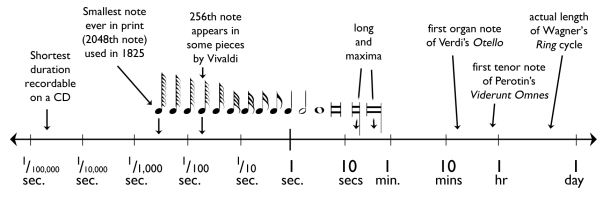
Figure 1: Lengths of different note values at M.M. qtr. = 60.
(with actual CD frequency and Ring lengths for reference)
In contemporary art music, composers have played with all extremes of lengths, but the most significant innovations in notation have come, as they did in the Middle Ages and Renaissance, in the notation of the most fleeting notes.[4] One of the most interesting case studies in the continuation of the medieval tradition of shorter notes comes in the American composer George Crumb’s string quartet Black Angels (1970), where, in the excerpt shown in Example 2, he uses a time signature of 7/128 in measure 2--written with the denominator as a note--along with the almost as equally unusual 7/64 with each note receiving an equal accent, thus providing the shortest non-compound meter ever published.

Example 2: Unusually short beat values in George Crumb’s Black Angels.
Other unusual and brief meters appear occasionally in modern music. Karlheinz Stockhausen’s 1956 composition Zeitmaße uses meters that are nearly as short as Crumb’s, such as 2/32. Composers allied with the New Complexity school, including Brian Ferneyhough and Thomas Adès, have used meters such as 5/6 and 2/10 that allow “tuplet” values (in these cases, triplets and quintuplets) to be fundamental and independent units. Finally, though multiple simultaneous meters were used in the works of both Bach and Mozart, the metrical experiments of Conlon Nancarrow use multiple meters in ways that particularly stretch the definition of meter. His “Transcendental” Etude contrasts two canonic lines whose rhythms are in the ratio of the transcendental irrational numbers e to π.
I am particularly interested in these unusual ways of specifying beat and meter in today’s music because the same spirit of experimentation was at work throughout the Italian ars nova. The feeling that the resources of the past were insufficient to express the creative metrical impulses of the present dominated musical thought in the late Trecento and early Quattrocento. Over the next few blog posts I hope to show how.
[1] This post is adapted from part of an article "Changing Musical Time at
the Beginning of the Renaissance (and Today)" to be published by L. Olschki in an as-yet-unannounced surprise Festschrift in 2011.
[2] On attempts to measure the slowing of medieval musical time in terms of clock time, see Marco Gozzi, “New Light on Italian Trecento Notation, part 1”, Recercare 13 (2001), pp. 5–78.
[3] The source for these (and many other) extremes of musical notation is Donald Byrd’s excellent on-line resource. I thank him for many stimulating conversations on this topic. The score of Example 1 has been republished recently as Anthony Phillip Heinrich, The Sylviad, or, Minstrelsy of Nature in the Wilds of North America: opus 3, intr. J. Bunker Clark, Greenleaf, Wis. 1996. The term chromatic in the title of the piece refers not to notes out of the key, but to the amount of ink (or color) needed to express the short notes in the work.
[4] On recent uses of extremely long durations in recent music see Alex Rehding, “The Discovery of Slowness in Music,” forthcoming.
Seemingly from the first moment when music became measured (musica mensurata), it began to slow down. The earliest measured music, that of Leonin and Perotin, the twelfth and early-thirteenth century composers of Notre Dame, used the figure of the “long” as a basic value, to be paired up and combined into a maxima or duplex long, or to be divided into three breves. By the late thirteenth century, music had slowed to such an extent that the breve became the basic note value, and the semibreve, worth either one-half or one-third the value of the breve, sprang into use.[2] This word, semibreve, is still the most common name in the British world for the note that in the States is called the whole note. Because the process of slowing continued unabated, this note is now the longest value in frequent use. By the fourteenth century, the tempo of music had slowed sufficiently that a note even faster than the semibreve needed to be introduced. This note came to be called the minima or minim--still the British word for half note—-signifying that this was to be the minimum, that is, the final, indivisible smallest possible note. (The debates of the music theorists of the Trecento are echoed in the discussions of modern physics that postulate that time itself may move in discrete and indivisible minima, each lasting about 1/200,000,000,000,000,000,000,000,000,000,000,000,000,000,000th of a second.) But the force of the slowing trend could not be stopped: it was less than fifty years later that the first “semiminim” would appear. Its name embodies a contradiction, “half of the shortest possible note,” yet though it was an extremely fast note for its time, it eventually became our most basic beat, the quarter note.
The process of slowing itself slowed slightly during the fifteenth, sixteenth, and seventeenth centuries. Faster notes continued to be introduced, but the fundamental tempos of music changed little. There are exceptions, and in some of these cases the slowness of the fundamental beat and the speed of the shortest notes produced dramatic effects: tuplet 128th notes appear in Beethoven’s third piano concerto, 256th notes in a concerto by Vivaldi (F. IV. n. 5), and most exceptionally, 1024th notes (incorrectly notated as 2048th notes) in the little known “Toccata Grande Cromatica” from The Sylviad by Anthony Phillip Heinrich (ca. 1825), a piece that in its own continual slowing of the fundamental beat is a microcosm of all of the notated music history of the West.[3] (See Example 1).

Example 1: Anthony Phillip Heinrich, “Toccata Grande Cromatica,” excerpt, with 512th and 1024th notes (incorrectly notated as 1024th and 2048th notes) at the end of the example.
Between Perotin and Heinrich, there exists a range of time that is almost incomprehensible to our sense of how music unfolds. Within a single maxima, there are 1024 128th notes, and, as we have seen, even longer and shorter notes have occasionally been used. Example 2 shows (on a logarithmic scale) the amount of time various notes would take if they were all played at the same adagio tempo of one quarter note per second. Obviously it is absurd to use the entire range of note values in a single piece at a single tempo mark. In fact the pieces using the shortest notes tend to have the slowest tempos, and the contrary is true for pieces with the longest notes. But Figure 1 demonstrates the enormous pull towards expanding the range of rhythmic resources that composers have felt over the centuries.

Figure 1: Lengths of different note values at M.M. qtr. = 60.
(with actual CD frequency and Ring lengths for reference)
In contemporary art music, composers have played with all extremes of lengths, but the most significant innovations in notation have come, as they did in the Middle Ages and Renaissance, in the notation of the most fleeting notes.[4] One of the most interesting case studies in the continuation of the medieval tradition of shorter notes comes in the American composer George Crumb’s string quartet Black Angels (1970), where, in the excerpt shown in Example 2, he uses a time signature of 7/128 in measure 2--written with the denominator as a note--along with the almost as equally unusual 7/64 with each note receiving an equal accent, thus providing the shortest non-compound meter ever published.

Example 2: Unusually short beat values in George Crumb’s Black Angels.
Other unusual and brief meters appear occasionally in modern music. Karlheinz Stockhausen’s 1956 composition Zeitmaße uses meters that are nearly as short as Crumb’s, such as 2/32. Composers allied with the New Complexity school, including Brian Ferneyhough and Thomas Adès, have used meters such as 5/6 and 2/10 that allow “tuplet” values (in these cases, triplets and quintuplets) to be fundamental and independent units. Finally, though multiple simultaneous meters were used in the works of both Bach and Mozart, the metrical experiments of Conlon Nancarrow use multiple meters in ways that particularly stretch the definition of meter. His “Transcendental” Etude contrasts two canonic lines whose rhythms are in the ratio of the transcendental irrational numbers e to π.
I am particularly interested in these unusual ways of specifying beat and meter in today’s music because the same spirit of experimentation was at work throughout the Italian ars nova. The feeling that the resources of the past were insufficient to express the creative metrical impulses of the present dominated musical thought in the late Trecento and early Quattrocento. Over the next few blog posts I hope to show how.
Endnotes
[1] This post is adapted from part of an article "Changing Musical Time at
the Beginning of the Renaissance (and Today)" to be published by L. Olschki in an as-yet-unannounced surprise Festschrift in 2011.
[2] On attempts to measure the slowing of medieval musical time in terms of clock time, see Marco Gozzi, “New Light on Italian Trecento Notation, part 1”, Recercare 13 (2001), pp. 5–78.
[3] The source for these (and many other) extremes of musical notation is Donald Byrd’s excellent on-line resource. I thank him for many stimulating conversations on this topic. The score of Example 1 has been republished recently as Anthony Phillip Heinrich, The Sylviad, or, Minstrelsy of Nature in the Wilds of North America: opus 3, intr. J. Bunker Clark, Greenleaf, Wis. 1996. The term chromatic in the title of the piece refers not to notes out of the key, but to the amount of ink (or color) needed to express the short notes in the work.
[4] On recent uses of extremely long durations in recent music see Alex Rehding, “The Discovery of Slowness in Music,” forthcoming.
Labels:
George Crumb,
music,
musicology,
notation,
tempo
31 March 2010
Cantus scriptus: Technologies of Medieval Song
 | A two-day conference at University of Pennsylvania, November 19-20, 2010 will explore technology and medieval notation, both medieval notation as a technology in itself and new technologies used to study medieval musical manuscripts. I will be presenting on digital restorations, "bad" facsimiles (photos designed not to convey the look of the original, but instead facilitate further study), and how statistical models can help us estimate the number of French pieces of the late Middle Ages that once existed but now are lost. |
Labels:
medieval music,
music,
musicology,
technology
Subscribe to:
Comments (Atom)